How did I miss this very cool, interesting polyhedron? Glad to have just discovered this fascinating shape (with lovely rotating animation) on this post by “RobertLovesPi” here, with this commentary:
The Platonic Icosahedron has twenty faces which are equilateral triangles. In the Golden Icosahedron, twelve of those triangles (the yellow ones) have been replaced by acute, isosceles triangles with a leg:base ratio which is the Golden Ratio.
Here are a few other appearances of the golden ratio (a.k.a. golden proportion a.k.a. golden number a.k.a. golden section a.k.a. extreme and mean ratio a.k.a. divine proportion a.k.a. Phi (ø) or Tau (τ) proportion a.k.a. sacred cut, etc., and other synonyms for the ubiquitous (1 + √5)/2 ≈ 1.6180339887… number):
- Golden Triangle (featured 12 times in the Golden Icosahedron above) and in every pentagram and regular decagon with lines connecting vertices to its center.
- Golden Rectangle
- Pentagram
- Pentagon
- Lots of other instances throughout this website!
This unexpected golden ratio appearance first made my acquaintance at a sacred geometry conference hosted by Luke Gatto a few decades ago in Boulder, Colorado, and I shared it many years later here in 2011:
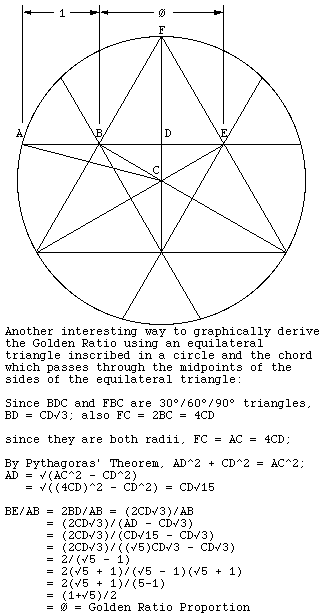
How to graphically derive the Golden Ratio using an equilateral triangle inscribed in a circle
and resurfaces here on a Quora post – and I’m copying the entire account verbatim; thanks, Johann!
Johann Holzel
Author has 4K answers and 1.1M answer viewsSome ratio has to satisfy a/b = (a+b)/a. The fact that this ratio should have such a simple continued fraction, involves √5 and therefore pentagons, has a special relation between its negation and inverse, etc., these must have all been surprising developments when each was first discovered (in many cases, by ancient Greek geometers—although apparently it, or √5, was also the first number proven to be irrational, which was even more surprising).
But nowadays, you learn most of those things together, and are immediately shown how they fit together, so there’s not much room for surprise.
And most appearances in nature make sense once you think about them. For example, there are cases where the most irrational logarithmic spiral is obviously the best to use, and the fact that it can be closely approximated by the arithmetically-simple Fibonacci spiral makes it unsurprising that evolution would hit on it multiple times.
(In fact, most claimed appearances in nature or in art are either not even close to ϕ at all, or are just boring cases of an artist who heard great art is supposed to be full of golden ratios so they followed what they thought they were supposed to do.)
So the most unexpected places are probably the ones that come from amateurs. And probably the most famous of these is the equilateral triangle inscribed in a circle, just because of how deceptively simple it is.
A 1983 article in American Mathematical Monthly consisted of basically this picture, accompanied by the word “Behold!”
A and B are the midpoints of two sides; extend the line from A to B out to the circle and the intersection is C.
The ratio of AB to BC is obviously somewhere around 1.6-ish just from visual inspection. So is the ratio of AC to AB.
But in fact, they’re identical, which means they’re both exactly ϕ, the golden ratio.
Why?
The golden ratio doesn’t just show up in triangles unless you put it there (e.g., the golden triangle is specifically designed as the isosceles triangle with the self-similar bisection), and that isn’t the case here.
This was discovered by George Odom, an amateur mathematician, who was in correspondence with famous geometer H.S.M. Coxeter. Coxeter wanted to see how many readers could work out why ϕ shows up here.
To get the answer, you have to notice that this chord looks like it can be used to construct a regular pentagon. Then you can complete the construction, and prove it’s exact via the chord theorem. And then there’s no mystery left—unlike triangles, pentagons are full of the golden ratio. (Coxeter just gave the constructed pentagon as the answer.)
That’s deeper than the kind of thing you’d expect from what looks like a simple recreational mathematics problem. And even after you get it, it’s still almost magical that something so with no obvious pentagons, or self-similar folds, or anything like that, gives you ϕ, so simply.

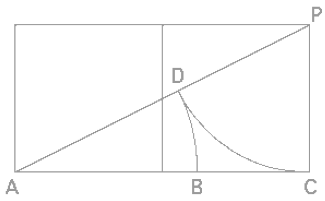




 Thanks to geometer colleague and dream researcher,
Thanks to geometer colleague and dream researcher, 
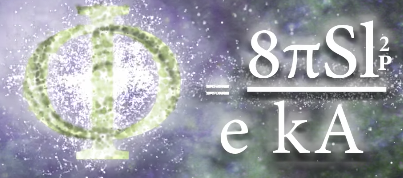
 Further fun Fibonacci forays for fascinating
Further fun Fibonacci forays for fascinating