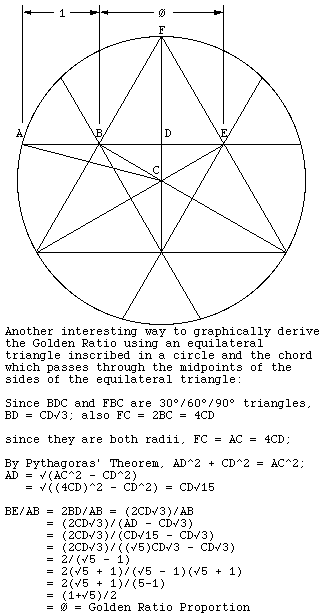
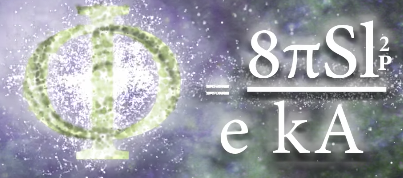Another interesting way to graphically derive the Golden Ratio using an equilateral triangle inscribed in a circle and the chord which passes through the midpoints of the sides of the equilateral triangle.
Search Results for: golden triangle
The Golden Icosahedron and other interesting Golden Ratio appearances
How did I miss this very cool, interesting polyhedron? Glad to have just discovered this fascinating shape (with lovely rotating animation) on this post by “RobertLovesPi” here, with this commentary:
The Platonic Icosahedron has twenty faces which are equilateral triangles. In the Golden Icosahedron, twelve of those triangles (the yellow ones) have been replaced by acute, isosceles triangles with a leg:base ratio which is the Golden Ratio.
Here are a few other appearances of the golden ratio (a.k.a. golden proportion a.k.a. golden number a.k.a. golden section a.k.a. extreme and mean ratio a.k.a. divine proportion a.k.a. Phi (ø) or Tau (τ) proportion a.k.a. sacred cut, etc., and other synonyms for the ubiquitous (1 + √5)/2 ≈ 1.6180339887… number):
- Golden Triangle (featured 12 times in the Golden Icosahedron above) and in every pentagram and regular decagon with lines connecting vertices to its center.
- Golden Rectangle
- Pentagram
- Pentagon
- Lots of other instances throughout this website!
This unexpected golden ratio appearance first made my acquaintance at a sacred geometry conference hosted by Luke Gatto a few decades ago in Boulder, Colorado, and I shared it many years later here in 2011:
How to graphically derive the Golden Ratio using an equilateral triangle inscribed in a circle
and resurfaces here on a Quora post – and I’m copying the entire account verbatim; thanks, Johann!
Johann Holzel
Author has 4K answers and 1.1M answer viewsSome ratio has to satisfy a/b = (a+b)/a. The fact that this ratio should have such a simple continued fraction, involves √5 and therefore pentagons, has a special relation between its negation and inverse, etc., these must have all been surprising developments when each was first discovered (in many cases, by ancient Greek geometers—although apparently it, or √5, was also the first number proven to be irrational, which was even more surprising).
But nowadays, you learn most of those things together, and are immediately shown how they fit together, so there’s not much room for surprise.
And most appearances in nature make sense once you think about them. For example, there are cases where the most irrational logarithmic spiral is obviously the best to use, and the fact that it can be closely approximated by the arithmetically-simple Fibonacci spiral makes it unsurprising that evolution would hit on it multiple times.
(In fact, most claimed appearances in nature or in art are either not even close to ϕ at all, or are just boring cases of an artist who heard great art is supposed to be full of golden ratios so they followed what they thought they were supposed to do.)
So the most unexpected places are probably the ones that come from amateurs. And probably the most famous of these is the equilateral triangle inscribed in a circle, just because of how deceptively simple it is.
A 1983 article in American Mathematical Monthly consisted of basically this picture, accompanied by the word “Behold!”
A and B are the midpoints of two sides; extend the line from A to B out to the circle and the intersection is C.
The ratio of AB to BC is obviously somewhere around 1.6-ish just from visual inspection. So is the ratio of AC to AB.
But in fact, they’re identical, which means they’re both exactly ϕ, the golden ratio.
Why?
The golden ratio doesn’t just show up in triangles unless you put it there (e.g., the golden triangle is specifically designed as the isosceles triangle with the self-similar bisection), and that isn’t the case here.
This was discovered by George Odom, an amateur mathematician, who was in correspondence with famous geometer H.S.M. Coxeter. Coxeter wanted to see how many readers could work out why ϕ shows up here.
To get the answer, you have to notice that this chord looks like it can be used to construct a regular pentagon. Then you can complete the construction, and prove it’s exact via the chord theorem. And then there’s no mystery left—unlike triangles, pentagons are full of the golden ratio. (Coxeter just gave the constructed pentagon as the answer.)
That’s deeper than the kind of thing you’d expect from what looks like a simple recreational mathematics problem. And even after you get it, it’s still almost magical that something so with no obvious pentagons, or self-similar folds, or anything like that, gives you ϕ, so simply.
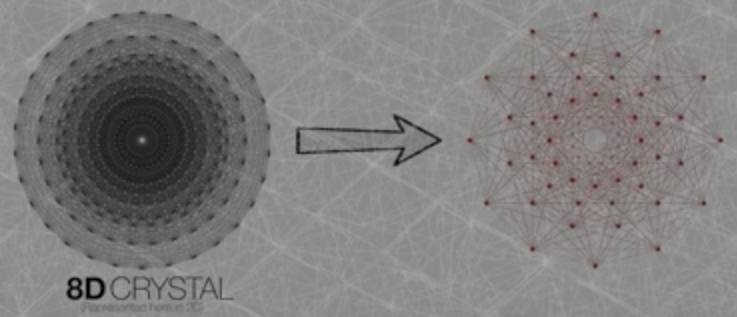
Golden Ratio Appears in 8D to 4D Quasicrystals, Black Holes, Consciousness Theory of Everything
 Thanks to geometer colleague and dream researcher, Ed Kellogg for alerting me to this very interesting (and fun) video “What Is Reality?” from Quantum Gravity Research (check out the lovely video loop of a slowly rotating polyhedron made of tetrahedra on their website’s home page) – in addition to meshing interconnections with our faithful omnipresent proportion, the Golden Ratio – also talks about higher dimensional geometric polytopes, Planck’s time and space constants, meaning, self-representing symbols, pixelation, geometric codes, non-local information … of course, consciousness – that ‘elephant in the room’ that mystics (not just in India) have been riding for millennia. :-)
Thanks to geometer colleague and dream researcher, Ed Kellogg for alerting me to this very interesting (and fun) video “What Is Reality?” from Quantum Gravity Research (check out the lovely video loop of a slowly rotating polyhedron made of tetrahedra on their website’s home page) – in addition to meshing interconnections with our faithful omnipresent proportion, the Golden Ratio – also talks about higher dimensional geometric polytopes, Planck’s time and space constants, meaning, self-representing symbols, pixelation, geometric codes, non-local information … of course, consciousness – that ‘elephant in the room’ that mystics (not just in India) have been riding for millennia. :-)
“The (8-dimensional) E8 Lattice … to generate that 3D quasicrystal, the substructure at the pixelated fabric of reality, we project this 8D crystal to 4D, and then we convert that to 3D. … just like the basic shape of the 3D cubic lattice is the cube, the cell shape of the E8 lattice is an 8D shape with 240 vertices. We call it the Gosset Polytope. When the Gosset Polytope is projected to 4D, it becomes two identical shapes of different sizes. The ratio of their sizes is … 0.618 (the Golden Ratio.)”
The video – after mercilessly exploding a cubic lattice made of Zometool, tsk, tsk! :-) – then references the appearance of the Golden Ratio in an equilateral triangle inscribed in a circle which we have documented on this website for many years.
“The Golden Ratio may be the fundamental constant of nature. … It is weirdly ubiquitous in the universe, appearing everywhere from the quantum to celestial scales. … it appears in black holes. The golden ratio is the precise point where a black hole’s modified specific heat changes from positive to negative. Ø = (M^4) / (J^2) … and it is part of the equation for the lower bound on black hole entropy. The golden ratio even relates the loop quantum gravity parameter to black hole entropy. Ø = 2 ^ (π?) … Why does this support the claim that the golden ratio is the fundamental constant of nature? Because a theory of everything must unite general relativity with quantum mechanics and a black hole is where these two theories converge at their limits.”
“Meaning is subjective and requires choice.” … Seems like physics is treading on metaphysical turf again. Fun! :-)
To dive a bit deeper into the projected polyhedral shape (which evidently resolves to an icosidodecahedron), check out this cool video – featuring Klee Irwin of Quantum Gravity Research – (“The 20-Group Twist”.)
For further detail, check out this video: “Quantum Gravity Research: an Overview Presented by Klee Irwin.”
“I felt glad to see this model incorporates E8 theory. I met Garrett Lisi when I attended his presentation on E8 theory (“An Exceptionally Simple Theory of Everything”) when I went to the 2010 Joint Mathematics Conference in San Francisco years back and felt quite impressed, but had heard nothing since. (See attached paper and check out this video link: https://www.youtube.com/watch?v=-xHw9zcCvRQ ).
I really enjoyed QGR’s ”What Is Reality” video, as it brings together a whole set of variable’s I’ve had an interest in – sacred geometry, consciousness, the golden ratio, the universe represented in a pixilated interface, derived from a non-local beyond time and space information matrix code, etc. all integrated into one congruent and entertaining presentation.
I especially found it quite cool that the golden ratio pops up as the ratio between the two sizes of the projection of the 8D Gosset polytope (from E8 theory) onto 4D – I’d never heard of that.
… check out this paper also: “Quantum Walk on a Spin Network and the
Golden Ratio as the Fundamental Constant of Nature,” http://www.quantumgravityresearch.org/wp-content/uploads/2017/04/quantum-walk-spin-31.pdf
One possibly important insight that occurred to me. The narrator talked about tetrahedrons as fundamental units (“physical reality pixels”), with each of them having different states. This reminded me of Donald Hoffman’s Conscious Agents, CAs, which he represented in a first rough approximation as triangular shapes/processes, functioning analogously in a manner somewhat similar to Turing machines:
From “Objects of Consciousness” (https://www.academia.edu/8227575/Objects_of_consciousness),
Even this simple model of interacting hierarchies of CAs leads to the identification of “a wavefunction ψ of the free particle with a harmonic function g of a space-time Markov chain of interacting conscious agents.”As a next step, bringing in another dimension of processing for more complex CAs, one would add another point to create higher dimensional tetrahedral CAs (“TCAs”), as it would add one more fundamental point, and three more communication channels might lead to the emergence of many more equations from the interaction of hierarchies of more complex TCAs. If so, what might that additional “point” represent, and what might the communication channels ? Something I find quite fun to think and to speculate about!
This has already given me ideas about what an upgrade of the “Beyond the Matrix: Conscious Realism and Lucid Being” workshop that I just gave at the Anaheim IASD conference might additionally include, in version 2.0. <g>”
Small Stellated Dodecahedron animation
The Small Stellated Dodecahedron – a classic three-dimensional (pentagram-faced) “star” – makes a wonderful fractal seed. It is a stellation of a dodecahedron where each pentagonal face is capped with a pentagonal pyramid composed of 5 golden triangles, a you could call it a 3-dimensional 5-pointed star. Some years ago when I was dabbling with POV-Ray, I made this primitive, rough study (with low resolution and lighting that didn’t quite do it justice) of a Small Stellated Dodecahedron fractal which is made by replicating smaller versions of itself and overlaying them on each of the 12 “arms” of the original, then doing this recursively as many times as your patience, resolution, etc. allows!

Here is a link (Math Monday: Fractal polyhedra clusters) to a rotating animation of a Small Stellated Dodecahedron fractal, which is one of the four Kepler-Poinsot Solids (all of which are featured with fold-up patterns (and more examples) in Sacred Geometry Design Sourcebook (SGDS):

Sacred Geometry interview with CA Brooks
CA Brooks, who hosts the “Simple Tales” show on 12Radio, interviewed me on August 26, 2014. We talked about the origins and history of sacred geometry in art, architecture and nature, the 5 Platonic Solids, dimensions, volcanos, symbols, the Great Pyramid at Giza, Egypt, the seven Hermetic Laws of antiquity, golden rectangles, golden triangles, spirals, the vesica piscis, and much more. This show was evidently selected as the “Producer’s Choice of the Week”; what fun! Enjoy! :-)
I also was on CA’s other show (about A Course In Miracles) on Aug. 22, 2014; more details and the audio archive for that interview here.