Sacred Geometry Media Resource Blog
In a recent post, I shared a few photos and a bit of the fun I had at the Zometool manufacturing facility near Boulder, Colorado, thanks to Carlos Neumann, Paul Hildebrandt, Jim Hausmann and other Zome enthusiasts. Not long after, Paul sent me these great photos of the completed installation at the Denver Art Museum. Thanks, Paul! :-) What a lovely geometric sculpture!
I just found this post in the archives of my personal blog here, which properly belongs on this site, so I’m reposting on GeometryCode.com. As mentioned toward the end, I am MOST grateful for all the support everyone has given me over the years since my first book (Sacred Geometry Design Sourcebook) was initially published in 1997 and the first website to support it shortly thereafter. The article gives some specific details about the images in the book, and I’ve added a couple of notes on pages 154 and 167 in response to an inquiry from a reader in Holland this morning. Here’s the post, with additions:
=== === ===
30Jan2007 09:17 AM Filed in: Geometry-Math
Today’s post is an email conversation I had with a visitor to the intent.com website that I probably could have written a decade ago, so this might be useful to those of you who already have purchased a copy of the book (and thanks to all of you who have supported me in this way over the years!) There are a few other goodies on my site map that might also be of interest.
=================================
Hi Julian:
Many thanks for your inquiry. I got so involved with the reply, that I’ve decided to post it on my blog for today, as well as in this email; I’m grateful that you asked the question, so now I can answer it for the world
On 30 Jan 2007, at 6:54 AM, Julian wrote:
Dear Bruce
I was reading your web pages about your book SACRED GEOMETRY DESIGN SOURCEBOOK and I wondered if you could tell me whether the book provides the reader with details of how to draw the 2-D patterns for themselves or whether they are just templates without such instruction.
The simplest answer is “yes and no”, depending on which of the 1300+ images you’re referring to.
————————————
The detailed answer is (here goes!) that I cover some of the philosophy and underlying
math, concepts and archetypal ideas in the beginning of the book, and provide a
generous assortment of references in the back of the book. For the remainder
(majority of the 256 pages), I give the images as much room as possible so that
not only can the patterns be photocopies easily (I went with spiral binding just
for that reason), the image quality would be as high as possible for an 8.5″ by 11″ format.
Some of the illustrations give step-by-step procedures (in graphical form,
assuming some basic familiarity with how to use a compass and straightedge), such as:
page 44 (showing how “unit cells” for the tiling patterns can be used to create an enormously
expanded variety of additional patterns by recognizing how the space-filling shapes can be
varied; this applies to the “unit cell” examples on pages 16-43,
page 45 (showing how each of the patterns on pages 16-43 can embellished with fractal or
other inscribed detail for each of the polygons for an infinite (literally!) variety of possible
variations, (which actually also applies to the majority of the remaining images in the book;
page 237 gives a 3D example of this),
pages 46-84 have either explicit (most of these pages) or simple to observe implicit “unit cells”
which show how these can be created in a great variety of ways,
page 84 (Pentagon Rotation Grid) gives the 73.2% proportion crucial to the exact construction of this pattern,
page 85 (Genesis of the Seed of Life) shows the step-by-step “compass only” construction of this important
and universal pattern,
page 86-95 (variations on Seed of Life and Flower of Life) show how once the Seed of Life is constructed,
so many other patterns can be easily derived – Flower of Life, Hexagonal Grid, 2nd Harmonic Overlay
(which is used in Mika Feinberg’s beautiful LightSOURCE screensaver animation; see my links page
at http://www.intent.com/bruce/links.html), Tree of Life, Fruit of Life, Heart and Ankh matrices, recursions,
Metatron’s Cube, etc.),
page 95: since the Dodecahedron is the most complicated shape to derive from Metatron’s cube, the top center
illustration on this page shows which vertices are used to create the “dodecahedron 2D shadow” with small
circles highlighted in the larger image,
page 96: The general instructions for creating Nested Inscribed Polygons appear on this page,
page 100-102: other examples of the crucial proportions needed to create these image either by hand or with a computer graphics program; numerous pages provide these instructions in the text without detracting from the space given to the images,
pages 104-105, 110-113, 123-124, 128, 130, 138-139, 144-145, 155, 163, 166, 171, 176-180, 182-187: all have instructions and details on how to create the images,
page 146: very detailed step-by-step instructions for inscribing a pentagon within a circle,
page 147: very detailed step-by-step instructions for inscribing a pentagon starting from one side of a given length,
page 154: Follow the steps on page 146, making a circle with an inscribed pentagon. Extend the lines of the pentagon to make a pentagram (5 pointed star). Extend lines from the center of the pentagram through the inner vertices to make a decagon with the outer pentagram vertices defining 5 of the 10 decagon vertices. Extend the lines of the decagon to generate the lines that become the next ‘ring’ of flattened (non-regular) pentagrams. Noticing the parallel lines and intersections, one can generate fractally nested flattened pentagram rings outward or inward in either direction.
page 156: very detailed step-by-step instructions for creating a golden rectangle (including “whirling squares and more),
page 156: very detailed step-by-step instructions for dividing a line by the golden ratio,
page 157: very detailed mathematical information about golden ratio progressions and powers, illustrated graphically,
page 167: Make a pentagram (following the steps on pages 146 or 147), then use 1 ‘arm’ of the pentagram (a Golden Triangle.) Alternately, you can make a golden rectangle, or just divide a line segment by the golden ratio (both on page 156) and then use your compass to make a golden triangle with these proportions. Once you have the golden triangle, set the compass to the small side length and swing an arc from one of the bottom vertices (intersection of two different-length sides) to one of the longer sides. Draw the line (same length as the short side) to the new intersection and you have the first smaller nested fractal golden triangle. Just keep repeating this process to make smaller golden triangles, each with side lengths 1/phi times the original.
page 188: shows how the Parthenon at the Acropolis in Athens, Greece incorporates the golden ratio
page 189: an amazing amount of data on this page about the Great Pyramid at Giza, Egypt showing phi (golden ratio) and pi proportions, and the proportions of the so-called “King’s Chamber” although the so-called “sarcophagus” (granite box) within is too large to fit through the only passage leading into that chamber, which violates the generally accepted funerary rite theory,
page 190: the classic “Measure of Man” (Vitruvian Man) by Leonardo daVinci, copied around the world, showing the golden ratio proportions in the human body,
page 191: the only known CAD drawing adaptation (to my knowledge) of Leonardo’s “Ideal Church” sketch,
page 192: detailed specifics about the Shoemaker’s Knife of Archimedes, giving several variations all showing the mathematical principle,
page 194: details of the geometry of the classic 1991 Barbury Castle, England crop circle formation,
page 195 and page 52: the details of the geometry encoded in the Sri Yantra (a classic Hindu mandala) and the cross section of the Great Pyramid at Giza, Egypt (also the “squaring the circle” conundrum), both with a 1-Phi-Square Root of Phi triangle which has a 51 degree, 51 minute slope,
page 196: numerous details common to the 5 Platonic and 13 Archimedean Solids,
pages 197-214; numerous details specific to the 5 Platonic and 13 Archimedean Solids, including how the insphere/intersphere/circumsphere/side length proportions are calculated,
pages 215-224: similar details specific to the 4 Kepler-Poinsot solids, the Star Tetrahedron (a.k.a. Stella Octangula) and related polyhedra,
pages 225-229: numerous graphics showing how the Platonic Solids relate to each other in a myriad of fascinating (awe-inspiring, really!) ways,
pages 230-235: numerous relationships between 3D polyhedra with 5-sided symmetry and the “shadow” they cast on a decagon (10-sided polygon), with construction details,
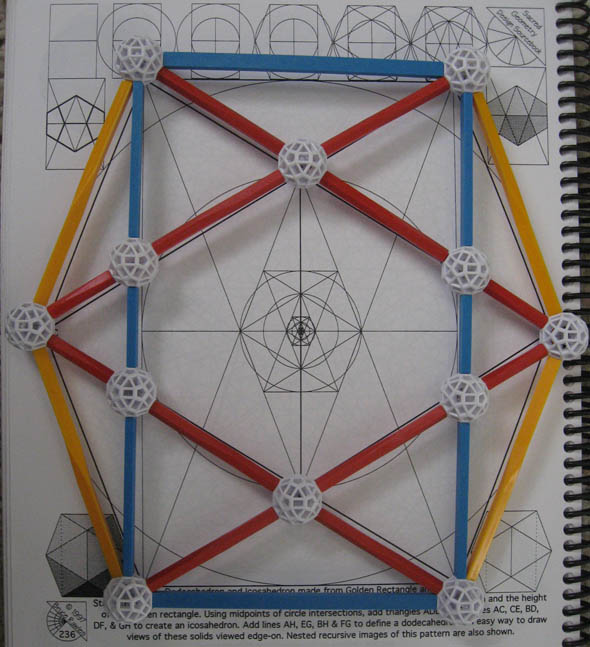
page 236: step-by-step instructions on creating an accurate drawing of the Icosahedron and Dodecahedron starting from a Golden Rectangle,
pages 237-255: generous appendices for hands-on explorers of all ages and levels of experience, including tables and charts of regular polygon angles, apothem, radius and side ratios and areas, radius ratios by coordination number for Ionic Chemical Bonding (which relates to properties of materials at the molecular and planetary levels), Fibonacci Numbers, Perfect Right Triangles (when I put the book together, I wasn’t aware of the Phi-1/Phi-Square Root of 3 Right Triangle that Mike Green of British Columbia introduced me to), Prime Numbers, extensive tables with all sorts of data on the Platonic and Archimedean Solids (useful for a variety of purposes, including model construction and computer simulation and animation, a map of planet Earth showing superimposed Platonic Solid Vertex Latitudes and (example) Longitudes, a fun stereogram with 6 Small Stellated Dodecahedra (there, I gave the clue away , a short bio of myself, 3 pages of bibliography (more on my books and links pages and blog), and unique graphical index to all the illustrations in the book. Whew! I’d almost forgotten how much I packed into this labor of love over a decade ago!
Many of the 1300+ images are somewhat self-explanatory graphically (especially if you have created the basic shapes like the Seed of Life, Golden Rectangle and a few others by hand with compass and straight-edge, which I highly recommend for anyone as mentor Keith Critchlow so aptly reminded me when reviewing my original manuscript)…
… and of course, if you are finding re-creating one of the patterns challenging, I’d be happy to answer other questions via email that I can share with other enthusiasts on my blog (which I’ll do with this reply; thanks for asking!
I’m also working on a number of related projects that will complement the book with video “hands on” procedures, etc. Stay tuned!
I recently had an email inquiry (and then a follow-up technique) from a reader of Sacred Geometry Design Sourcebook about how to replicate the “Flower of Life – with Second Harmonic overlay” illustration on page 87 using classic straightedge and compass techniques. Here is her illustration, with comments. The basic technique is to subdivide the underlying hexagonal/equilateral triangle grid by the number of the harmonic desired. Thanks to SEEW from Maryland for the contribution!
Recently, I had the pleasure of visiting the Zometool factory in Longmont, Colorado.
There, my favorite (hands down!) geometric toy, er, I mean modeling system, is manufactured. Paul and Carlos gave me a tour of the amazing technology where these wonderful plastic components are made by the gazillions. The secret of the hub, rumor has it, is the trained microscopic radiolaria that already understand the necessary geometry and amazingly eat away the parts of the hub that don’t look Zome-ish. You’re not buying that idea? Oh well… maybe there’s more to it than that… :-)
The primary purpose of the day’s festivities was to begin assembling circular ‘rosettes’ (note the white quasi-circular shapes with 6 yellow hubs in some of the photos) to be further assembled into a new art piece for the Denver Art Museum. (Stay tuned for updates on the blog page.) Here are a few photos from the fun, collaborative day with great music provided by Paul’s daughter Lizzy, and excellent Zometool assembling fuel provided by Carlos and others. I’m looking forward to seeing the finished project at the Denver Art Museum! :-)
Zometool, with the addition of green struts, can build many of the designs – both 2 and 3 dimensional – that appear in the pages of Sacred Geometry Design Sourcebook (SGDS) and other 2D and 3D models. Now, more than ever, this superlative modeling system (which is also the coolest toy in the geometric Universe, in my opinion) is a fabulous complement to Sacred Geometry Design Sourcebook.
The green struts allow for square root of 2 proportions relative to blue struts, which allow shapes like tetrahedra, octahedra, star tetrahedra, several more Archimedean Solids and MUCH more to be built. Amazing how adding another proportional system to the prior version seems to add many dimensions to the possibilities. (BTW, the feline model within the model is Cooper, our new kitten.)
Here are examples of some of Zometool models that appear in the pages of Sacred Geometry Design Sourcebook. I’ll be adding to these as I go on, so look for announcements in the monthly bulletin about updates to this page. This example, from page 236, shows the 2-D projection of icosahedral and dodecahedral cross-sections, and the underlying golden rectangle and golden-ratio-based geometric proportions.
