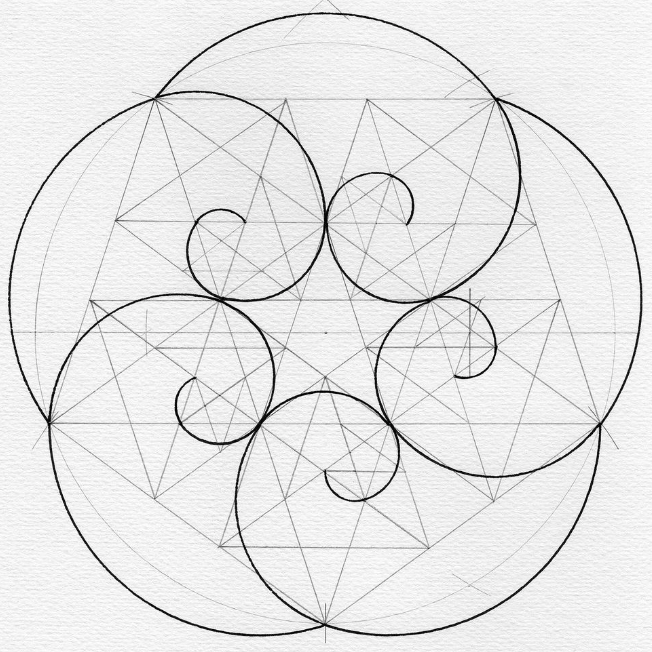
At the end of last month’s post we gave this example of non-Euclidean geometric art inspired by M. C. Escher’s pioneering graphics which explored various geometries and illusory perspectives.
Also noted in last month’s post, here’s a still image related to a scene in the movie “Inception” that had a physical implementation of an impossible (never-ending) staircase; our limited geometric perspectives can deceive us:

Since there’s no point in “reinventing the wheel” I’ll quote from Wikipedia’s definition for non-Euclidean geometry, also since I’m a novice in that field, but an admirer of art and imagery inspired by that geometry that stretches our imaginations:
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises by either replacing the parallel postulate with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry.
The principles below (from the next section in the Wikipedia page) reveal how the behavior of parallel and perpendicular lines differs in two common non-Euclidean realms; Hyperbolic Geometry and Elliptic Geometry: with a graphic demonstrating how if we don’t make certain Euclidean assumptions about space (e.g. parallel and perpendicular line behavior) such as the requirement that the sum of the angles of a triangle add up to 180°.
The essential difference between the metric geometries is the nature of parallel lines. Euclid‘s fifth postulate, the parallel postulate, is equivalent to Playfair’s postulate, which states that, within a two-dimensional plane, for any given line l and a point A, which is not on l, there is exactly one line through A that does not intersect l. In hyperbolic geometry, by contrast, there are infinitely many lines through A not intersecting l, while in elliptic geometry, any line through A intersects l.
Another way to describe the differences between these geometries is to consider two straight lines indefinitely extended in a two-dimensional plane that are both perpendicular to a third line (in the same plane):
-
In Euclidean geometry, the lines remain at a constant distance from each other (meaning that a line drawn perpendicular to one line at any point will intersect the other line and the length of the line segment joining the points of intersection remains constant) and are known as parallels.
-
In hyperbolic geometry, they diverge from each other, increasing in distance as one moves further from the points of intersection with the common perpendicular; these lines are often called ultraparallels.
-
In elliptic geometry, the lines converge toward each other and intersect.
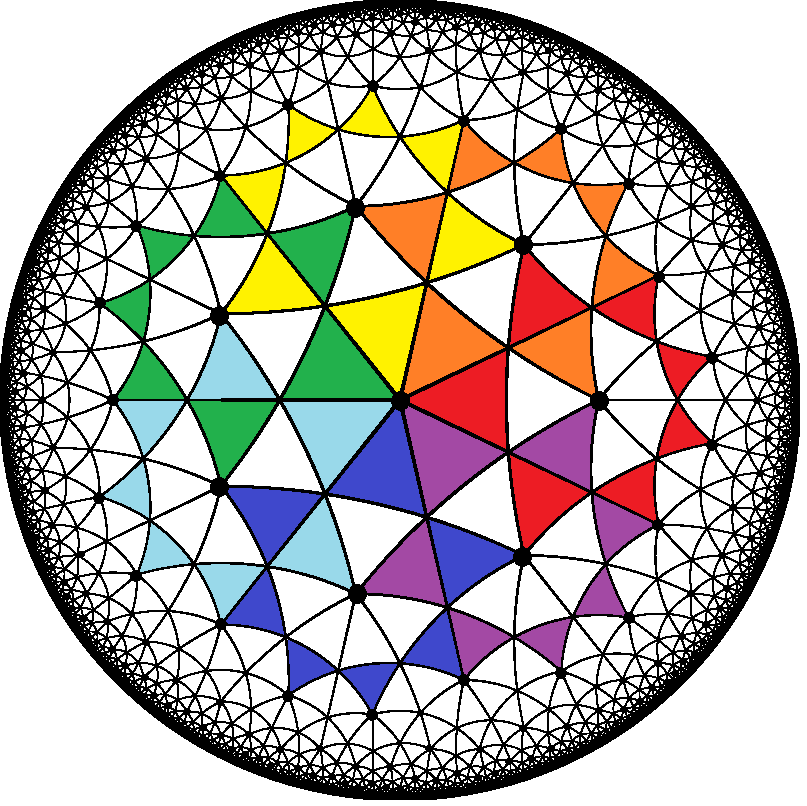
Here’s a simple graphic that gives a hint about the fundamentals of these mind-warping geometries that might be akin to warm-up exercises for four-dimensional (and beyond) geometries and polytopes, which we like to explore on this website now and then.

By Cmglee – Own work, CC BY-SA 4.0, Link
Here’s an example of hyperbolic geometric art:

Here’s an astronaut’s perspective example of how the sum of the angles of a non-Euclidean triangle can add up to more than 180° on the surface of a spheroid (our beloved planet):

For further exploration and many more wonderful and artistic images, I recommend this article “The Use of Non-Euclidean Geometry in Art” on the naiadseye blog …
and this post “Non-Euclidean Geometry Art August 4, 2014″ on “Harrison Hartle’s Art/Music/Theater F200 blog.”
The latter has this excellent TED talk video about “The beautiful math of coral” by Margaret Wertheim (2009); I first learned of this fascinating realm of modeling coral reefs (and many other “hyperbolic geometry” life forms with crochet hooks) from my colleague Libby M. in Oregon at a Geometers meeting about 20 years ago who had made and shared several knitted models inspired by this work:
Margaret Wertheim (in the video above) references the work of Froebel, an educational pioneer featured on this website. Froebel-inspired products are available from RedHen Books and Toys featuring unique, hard-to-find educational materials, toys and books such as Bradford Hansen-Smith’s circle folding videos, books and supplies.
In addition to the other affiliates on the GeometryCode.com website featured in the sidebar on every page that help support this “labor of love” website, please check out Ka Gold Sacred geometry jewelry by artist David Weitzman including wearable geometric art including Flower of Life, Seed of Life, Golden Spiral, Fruit of Life, Vesica Piscis, Star tetrahedron “Merkaba”, Fibonacci Whirling Squares Spiral “Phi”, Metatron’s Cube, Chambered Nautilus, Labyrinth, Torus Tube, Tetractys, Sri Yantra mandala, Tree of Life, and Hexagram (Star of David).
The Wolfram MathWorld page on Non-Euclidean Geometry also has many pertinent links and resources.
The Bridges organization has more related material on the subject of mathematical art.
In case you still need a 2025 calendar, there are 10 months left in the year as of the date of this post, and 2025 calendars are still available – as well as my over-quarter-century-old timeless classic reference book, Sacred Geometry Design Sourcebook – Universal Dimensional Patterns, heavily inspired by Escher, and other geometric luminaries.
 In a recent
In a recent