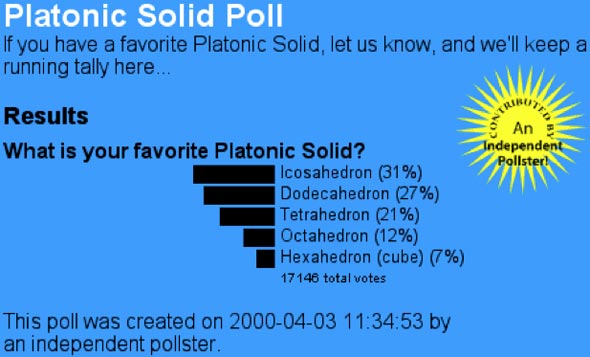
Musing about how the interpretations of our physical senses are often misled by optical (and other) illusions, I was reflecting on being inspired decades ago by the classic M. C. Escher images in the book (The Graphic Work of M.C. Escher Introduced and Explained By the Artist Paperback – January 1, 1973
by M. C. Escher). The cover of this Escher book features an image of a small-stellated dodecahedron with cutouts in half of the lower portion of each triangular face of each stellating pentagonal pyramid permitting polychromatic reptile heads and limbs to protrude (Gravity, June 1952. Lithograph and Watercolour.) Many of Escher’s illustrations demonstrate these sensory deceptions – which can be beneficially used to inspire a willingness to see things from multiple (open-minded) perspectives – such as images in his Impossible Constructions and Mathematical galleries and other classic images employing space-filling tessellation patterns and numerous instances of multiple simultaneous perspectives. In addition to an early introduction to Platonic Solids, Archimedean Solids, stellations, and more in the polyhedral realms, Escher’s pioneering visionary art seemed to suggest to me the value of exploring perspectives beyond what our unreliable senses (and our misinterpreting minds) report and stoked a curiosity to explore realms beyond ordinary viewpoints. My other primary blog is devoted to these metaphysical explorations.
Examples which show the distortions of our sensory misinterpretations include these images (I haven’t copied the images due to copyright requirements, so please tap the links on this post to check out these example Escher gems (many more in these extensive archives: Selected Works by M.C. Escher):
- Balcony. July 1945, Lithograph (a coastal condo scene where the center “bulges” out in fisheye lens fashion)
- Three Spheres I. September 1945, Wood Engraving. (I had a vibrant fluorescent “black light” poster of these stacked spheres on my wall in high school)
- Reptiles. March 1943, Lithograph (including a 3D dodecahedron and a 2D tiling (tesselation) pattern of tiled reptile shapes)
- Up and Down. July 1947, Lithograph (staircase/balcony composition combining bird’s eye and worm’s eye views of the same scene blended into one)
- House of Stairs. November 1951, Lithograph (an impossible realm of stairs crawling with multi-legged creatures that can crawl or spiral roll)
- Relativity, July 1953, Woodcut (another impossible realm of staircases)
- Sun and Moon. April, 1948, Woodcut, printed from four blocks (Solar/lunar motifs overlap with space-filling birds)
- Double Planetoid. December 1949, Wood Engraving printed from four blocks (star tetrahedron made from an “organic” tetrahedron and a “man-made” tetrahedral world that interpenetrate but do not appear to touch)
- Order and Chaos II. August 1955, Lithograph (featuring a small stellated dodecahedron with pentagrams on the pentagonal bases)
- Three Worlds, December 1955, Lithograph (leafs float on the surface of a fish pond reflecting bare winter tree branches which also seem like roots); this image was used as the original album cover for the Beaver & Krause vinyl album “In A Wild Sanctuary” which you can hear here, combined with their more recent album, Gandharva (celestial musician). Fascinated by the idea of musically interesting harmonics and proportions, I made (using a FORTRAN program) a spreadsheet using the CDC3400 our high school had access to once a week showing resonant frequencies and harmonics of the Grand Gallery of the Great Pyramid at Giza, Egypt (see other internal references to the amazing geometry of this pyramid) and other accessible chambers. On two occasions, I visited Beaver’s Los Angeles recording studio in the early 1970s and planned to join him to record electronic (Moog analog synthesier) music in the Great Pyramid at Giza, Egypt in fall 1973, but this trip never materialized, as the Middle East political situation then was hardly conducive to travel. In November 1992 (19 years later) I was able to explore the interior of the Great Pyramid and record some flute music by Gregg Braden (his website) with my wife Nancy and 18 others on a tour led by Braden.
- Print Gallery, May 1956, Lithograph (a recursive image of an art gallery where the interior columns become exterior posts of an overhanging roofline); this is the image that reminded me of non-Euclidean Geometry and revisiting Escher’s art for this post.
Here is a close-up of Escher-inspired tiles that adorn the front yards of at least two local homes in Green Valley, AZ; photographed on nearby neighborhood walks during the past 18 months.

For further exploration, check out:
- the official M. C. Escher website
- the M. C. Escher Wikipedia page
- Wolfram MathWorld references to Escher, such as Penrose Stairway, Freemish Crate, Impossible Figure, etc.
- Lessons in Duality and Symmetry from M.C. Escher
- The Influence of the Perspectives of M.C. Escher … just for starters!
The end of the last article above reminded me that there’s a scene in the movie “Inception” (a fave flick) that had a physical implementation of one of these impossible (never-ending) staircases. featured in popular Escher image:
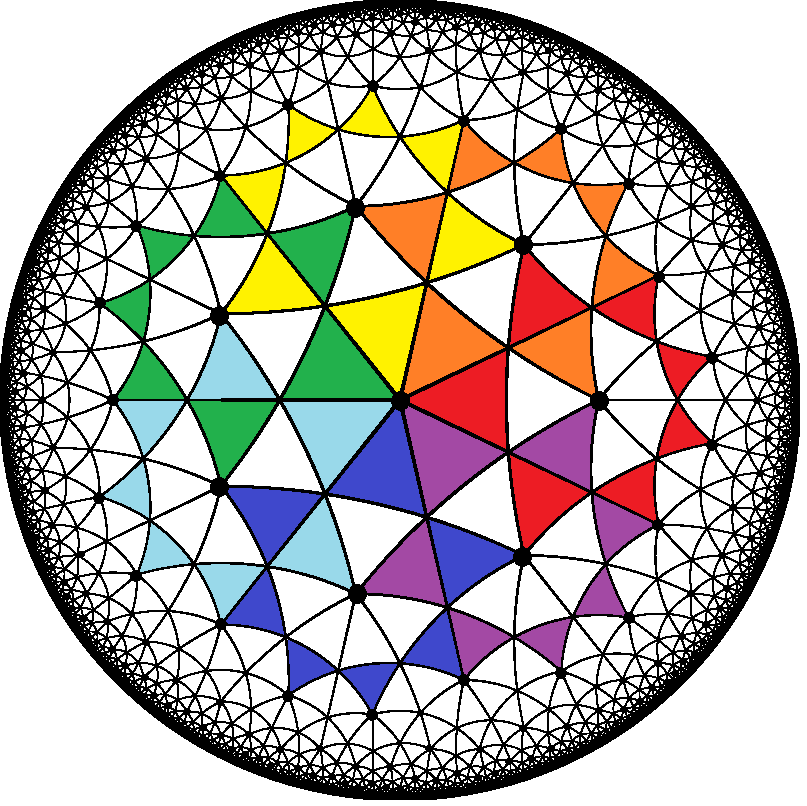
Escher’s art also explored Non-Euclidean Geometries, which will be featuring in next month’s post. The art below reflects an example of an Escher-inspired Non-Euclidean geometry.
In case you still need a 2025 calendar, there are 11 months left in the year as of the date of this post, and 2025 calendars are still available – as well as my over-quarter-century-old timeless classic reference book, Sacred Geometry Design Sourcebook – Universal Dimensional Patterns, heavily inspired by Escher, and other geometric luminaries.




 In a recent
In a recent