How to make a model of Nested Platonic Solids with Zometool

I recently disassembled a favorite Nested Platonic Solid model (for transport) and decided it might be helpful to take a few photos of the process and present them in reverse order, to help anyone wanting to use Zometool to build this unique geometric nest of the 5 regular polyhedra attributed to Plato. About a decade ago, I made this Infinite Recursive Animation of these Nested Platonic Solids and zoomed in for 3 full cycles of the loop to show the relationships between the five solids and some of the details that might be missed otherwise, so this post will complement that animation. Here’s a still frame from that animation that shows the 2 outermost polyhedra (the octahedron in light green and the icosahedron in dark blue):

frame from nested platonic solid animation showing octahedron-icosahedron golden-ratio vertex relationship — frame from nested platonic solid animation showing octahedron-icosahedron golden ratio vertex relationship

Here are all the Zometool struts and hubs you’ll need:

… and now we start by assembling the innermost polyhedron, the tetrahedron from these shorter green struts and white Zometool hubs:

green struts and hubs needed to make the outer octahedron: Nested Platonic Solids model using Zometool — green struts and hubs needed to make the inner tetrahedron model using Zometool

… adding the smaller blue struts and the ubiquitous white Zometool hubs to the green tetrahedron makes a blue cube (a.k.a. hexahedron); here we can see the √2 edge length proportion:

2 polyhedra; cube outermost - Nested Platonic Solids using Zometool — 2 polyhedra; cube outermost – Nested Platonic Solids using Zometool

Now adding these “roof caps” to each of the 6 square faces of the cube…

example of roof tents defining edges of dodecahedron outermost: Nested Platonic Solids model using Zometool

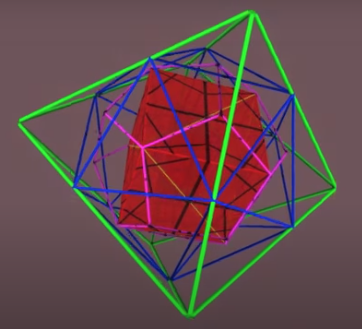
… we get a dodecahedron; see also page 229 in Sacred Geometry Design Sourcebook for an “exploded view” drawing in the lower-left corner of the page for additional reference.