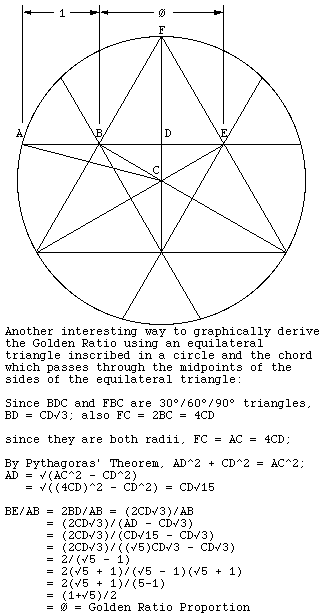
Another interesting way to graphically derive the Golden Ratio using an equilateral triangle inscribed in a circle and the chord which passes through the midpoints of the sides of the equilateral triangle.
Search Results for: golden ratio
Geometric Inspiration and Education
 Reflecting on the growth – explosion, really – of information available to us online compared to what we had access to just a few decades ago, I recalled that in the early 1970s when I was an undergraduate electrical engineering student at UC Davis, California, I used the card catalog in a long row of tidy wooden cabinets at the Shields Library – a building which covers an entire block of the campus – to look up everything I could find (at that time) on the Golden Ratio, Golden Number, Golden Section, Divine Proportion, Phi (ø) or Tau (τ) Proportion, Sacred Cut, Extreme and Mean Ratio, etc. and other synonyms for the ubiquitous (1 + √5)/2 ≈ 1.6180339887… value. This fascination was my response to a gift of two books – both with references to the golden ratio – from my mother who indirectly introduced me to this enthralling subject which later was popularized with the term “sacred geometry”:
Reflecting on the growth – explosion, really – of information available to us online compared to what we had access to just a few decades ago, I recalled that in the early 1970s when I was an undergraduate electrical engineering student at UC Davis, California, I used the card catalog in a long row of tidy wooden cabinets at the Shields Library – a building which covers an entire block of the campus – to look up everything I could find (at that time) on the Golden Ratio, Golden Number, Golden Section, Divine Proportion, Phi (ø) or Tau (τ) Proportion, Sacred Cut, Extreme and Mean Ratio, etc. and other synonyms for the ubiquitous (1 + √5)/2 ≈ 1.6180339887… value. This fascination was my response to a gift of two books – both with references to the golden ratio – from my mother who indirectly introduced me to this enthralling subject which later was popularized with the term “sacred geometry”:
- Secrets of the Great Pyramid by Peter Tompkins
- This Living Earth by David Cavagnaro
I found a few dozen books that led to other books and on and on into the mystical realms of the intersections of mathematics, ornamentation, art, music, architecture, history, and above all – mind. … But after checking out those books, I felt I had somewhat exhausted the more obvious references to this topic in this library. … Not anymore!
Fast forward a half-century; now googling Sacred Geometry, as of today (21 April 2022) we get a staggering 45 million results for this niche topic (including my evergreen minimalist GeometryCode Introduction to the subject now way past overdue for a revisit and update) and 481 million for the Golden Ratio!
The same curiosity still remains in my mind: What can be counted on that does NOT change? The laws of mathematics in general and geometry, in particular, seem relatively stable, fortunately, at least within the context of the Cartesian space-time paradigm. When I was in high school, I read Education and Ecstasy by George Leonard and I realized that to really dive deep and learn immersively, one needed to be motivated, inspired or at least have their curiosity seriously piqued or their assumptions about life challenged. Exploring some of the ideas that these readings opened up for me was enough!
Now there are a multitude of online offerings that can motivate young and old alike to explore esoteric topics like interconnectedness (e.g. quantum entanglement), geometric symbolism and synchronicities, and so much more. Another vital element that has a multiplying effect is FUN!
Here are a few quickly-found resources for educators and explorers in this realm (including teachers, home-schoolers) and philosophers of all stripes:
- A simple but engaging animation showing basic 2D geometries morphing from one to another:
Shapes – Learn 2D Geometric Shapes – The Kids’ Picture Show (Fun & Educational Learning Video) - 10 Geometric Art Explorations (Study measurement, area, fractions, and more!) … The graphic of color-filled intersections of simple 2D shapes on this page was adapted from the image below the “6. Frac-Geo-Bot” section on this page.
- … for about 23 million more links, try googling “geometric art science toys videos”
- or try these categories on the GeometryCode website: coloring books for adults, sacred geometry art, sacred geometry books, sacred geometry coloring books, sacred geometry toys … just for starters
Enjoy! :-)
Golden Mean Calipers revisited
From about 4:25 – 5:19 in this video, fine art instructor Ken Campbell reveals one of his 6 keys to designing great art – using the golden mean a.k.a. golden ratio a.k.a. sacred cut a.k.a phi proportion ≈ 1.618 (or its inverse which is roughly 62% – close enough for most small art projects – in laying out design concepts.
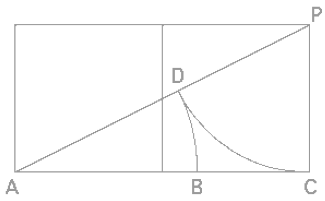
The ratio of AB to BC in the illustration below is in golden ratio proportion. (This “Dividing a Line by the Golden Ratio” illustration is from page 156 of Sacred Geometry Design Sourcebook – Universal Dimensional Patterns. That page also shows – with simple step by step instructions – how to make a golden rectangle (a more familiar classic construction, perhaps) using only a straightedge and compass:
I was working on another project in the office when I overheard these comments in the fine art YouTube video noted above that my wife, Nancy, was watching as she brushes up (pun intended) on techniques. I reminded her that my golden ratio compass was available for her art toolkit. The one I purchased a couple of decades ago (from Now and Zen of Boulder, Colorado, (c) 1997) appears to be no longer available, and the one I featured last year seems to be currently unavailable.
However, here are a few variations of golden ratio calipers that should work well. A couple of them also have an arm that locates the midpoint of the smaller length, and in the metal one, that additional arm’s location is reversible, so it can locate the midpoint of the longer length.
If you have artwork (2D, 3D or whatever) inspired by sacred geometry, and particularly that uses the phi (golden ratio) proportion that you’d like me to consider featuring on this site, please contact me! I enjoy sharing creativity from a wide range of media and artistic styles.
Penrose and other Tilings: periodic and aperiodic – video exploration

Kepler’s Model of the Solar System (nested Platonic Solids) and other fun and somewhat boggling geometric explorations unfold in this visually engaging video presentation about periodic … and aperiodic pentagonal tilings discovered by Roger Penrose, quasicrystals, and – of course – cameo appearances by the Golden Ratio and the Fibonacci Series. Enjoy! :-)
Thanks to Shaun L. for alerting me to this gem of a video!
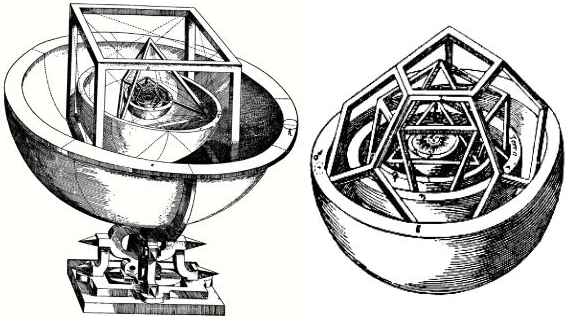
If you’d like to explore the various periodic tilings and/or Platonic Solids (both mentioned in the video above) and much more, check out my first book, Sacred Geometry Design Sourcebook: Universal Dimensional Patterns!
Stella Octangula projects Paul McCartney, Hendecagon architecture, Irrational Phi
 Another super quick, fun update for sacred geometry enthusiasts!
Another super quick, fun update for sacred geometry enthusiasts!
- Check out this fun, animated articulated model of Leonardo da Vinci‘s “Stella Octangula” (a.k.a. stellated octahedron or star tetrahedron – fold-up model here) making a cameo appearance as a holographic projector on a sci-fi Paul McCartney music video which seems inspired by Princess Leia’s classic hologram “Help me Obi-wan” plea.
- The image above shows the uncommon 11-sided (hendecagon) geometry from a lovely slideshow gallery of images from this article: India’s New Parametric Temple to Reinterpret Vernacular Design in Koppur.
- Starting with a clear explanation of how a flower might optimize seed spacing geometrically (with insightful animations) this Numberphile video shows why the Golden Ratio is so irrational.