All graphics on this page are from Sacred Geometry Design Sourcebook
- The Tetrahedron (4 sides)
- The Hexahedron (a.k.a cube, 6 sides)
- The Octahedron (8 sides)
- The Dodecahedron (12 sides)
- The Icosahedron (20 sides)
Sacred Geometry Media Resource Blog
by Bruce Rawles
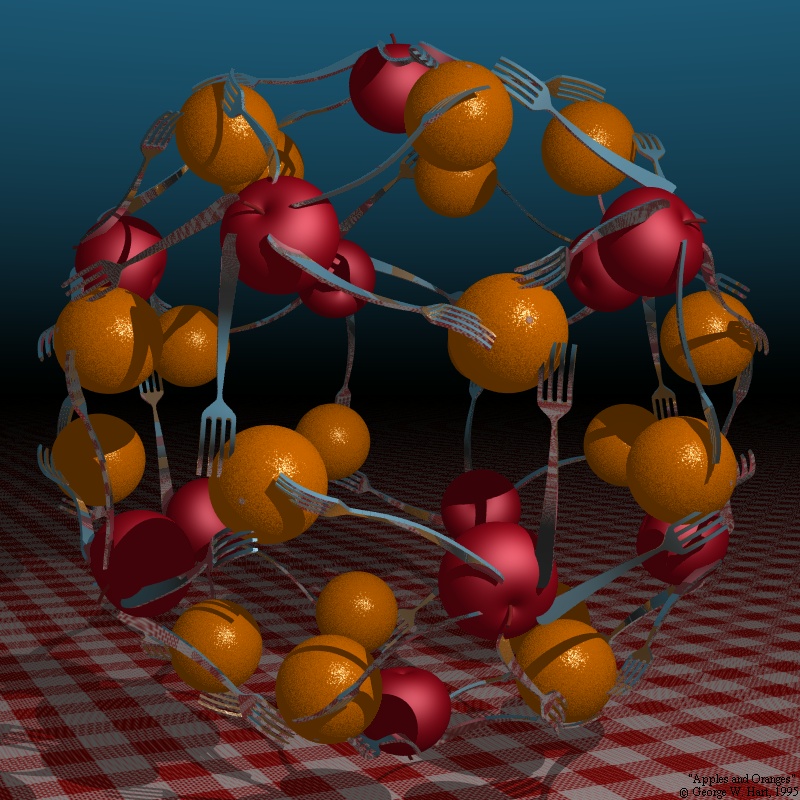
It’s time to revisit the work of other polyhedra enthusiasts. Of particular note (having crossed my digital path again recently) is George W. Hart who has shared some excellent resources along these lines (faces, vertices, etc.) for decades. Here’s one gold mine to explore: Virtual Polyhedra: The Encyclopedia of Polyhedra By George W. Hart. Here is part of the table of contents and highly recommended if you want to explore the genres and categories of polyhedra; lots of great imagery, rotatable 3D models (rotate them with your mouse), facts and details:
Perhaps the most well-known and ubiquitous polyhedral shapes have fold-up models (and related patterns) for the first 3 categories above in Sacred Geometry Design Sourcebook (SGDS pages 196-220) and also on this website for the 5 Platonic Solids and 13 Archimedean Solids as well as Illustrations of Platonic And Archimedean Solids, Math Tables for Platonic And Archimedean Solids (and much more about polyhedra on this website.

If you exhaust this generous resource (or somehow overlook a few gems) here are more of his contributions – the videos are particularly helpful if you want to replicate his constructions:
by Bruce Rawles
Musing about how the interpretations of our physical senses are often misled by optical (and other) illusions, I was reflecting on being inspired decades ago by the classic M. C. Escher images in the book (The Graphic Work of M.C. Escher Introduced and Explained By the Artist Paperback – January 1, 1973
by M. C. Escher). The cover of this Escher book features an image of a small-stellated dodecahedron with cutouts in half of the lower portion of each triangular face of each stellating pentagonal pyramid permitting polychromatic reptile heads and limbs to protrude (Gravity, June 1952. Lithograph and Watercolour.) Many of Escher’s illustrations demonstrate these sensory deceptions – which can be beneficially used to inspire a willingness to see things from multiple (open-minded) perspectives – such as images in his Impossible Constructions and Mathematical galleries and other classic images employing space-filling tessellation patterns and numerous instances of multiple simultaneous perspectives. In addition to an early introduction to Platonic Solids, Archimedean Solids, stellations, and more in the polyhedral realms, Escher’s pioneering visionary art seemed to suggest to me the value of exploring perspectives beyond what our unreliable senses (and our misinterpreting minds) report and stoked a curiosity to explore realms beyond ordinary viewpoints. My other primary blog is devoted to these metaphysical explorations.
Examples which show the distortions of our sensory misinterpretations include these images (I haven’t copied the images due to copyright requirements, so please tap the links on this post to check out these example Escher gems (many more in these extensive archives: Selected Works by M.C. Escher):
Here is a close-up of Escher-inspired tiles that adorn the front yards of at least two local homes in Green Valley, AZ; photographed on nearby neighborhood walks during the past 18 months.

For further exploration, check out:
The end of the last article above reminded me that there’s a scene in the movie “Inception” (a fave flick) that had a physical implementation of one of these impossible (never-ending) staircases. featured in popular Escher image:
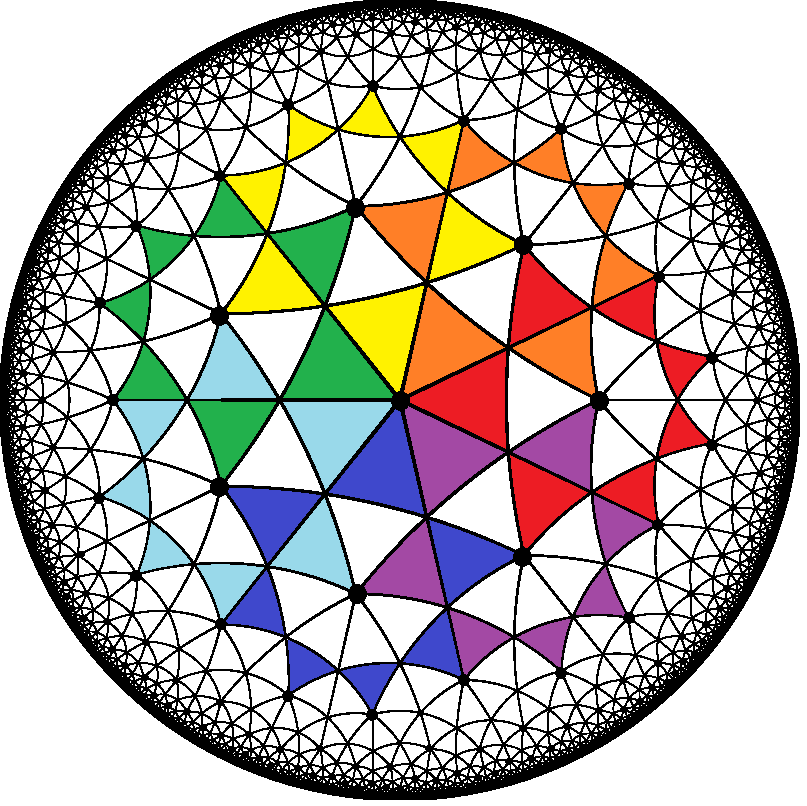
Escher’s art also explored Non-Euclidean Geometries, which will be featuring in next month’s post. The art below reflects an example of an Escher-inspired Non-Euclidean geometry.
In case you still need a 2025 calendar, there are 11 months left in the year as of the date of this post, and 2025 calendars are still available – as well as my over-quarter-century-old timeless classic reference book, Sacred Geometry Design Sourcebook – Universal Dimensional Patterns, heavily inspired by Escher, and other geometric luminaries.
by Bruce Rawles
Update 21 July 2024: We’ve been in Arizona for exactly a year today, and I still have a handful of German books to find homes for, so I’m re-dating this post in case anyone would like to purchase a book for only my shipping costs!
(Originally published 25Jun2023):
We’re making good progress toward moving to Arizona (mid-July 2023) so I’m anticipating having more time to do in-depth posts after our move. Meanwhile, I’d still like to lighten our load and not move these books yet another time… I’m offering (until mid-July, while supplies last) – limited supply; limited offer) asking only for my shipping costs (US only) or free if you happen to be on the central Oregon coast and can pick them up here in Yachats before we move! in the Tucson, AZ metro area and can pick them up.
I have a handful of both of my German-translated books:
(If you live in Germany, you’ll probably want to order the Bewusst malen – Heilige Geometrie book, still in print, directly from the publisher, Silberschnur Verlag, since the shipping from the USA to Germany is likely more than buying it locally.)
If you speak German or know someone who does and has the least interest in geometry, I am offering special FREE books (very limited supply) of both of these books if you cover my postage costs. If you live near Yachats, Oregon, Green Valley, Arizona, you can pick them up here and skip the postage expense. For details on these limited-time, limited-supply books, contact me.
Note that you don’t have to be able to read or understand German to enjoy either of these books, as they are both lavishly illustrated – FAR more imagery than text. Also, each copy of the out-of-print MDHG book has a unique set of die-cut fold-up models of the 5 Platonic Solids (included behind the back cover) that make a neat mobile if you add your own thread.

Please contact me before mid-July 2023 if you are interested in this special offer!


Here are a few more interesting geometry-related links (videos) that have crossed my path recently; several short introductory videos that add some useful and interesting additions to commonly cited facts:
by Bruce Rawles
Here’s an invitation to geometric artists (and enthusiasts) to share their creativity, explorations, and discoveries.
My wife Nancy – an artist who for years has worked mostly in acrylics – has recently been making some lovely (ceramic/clay) art while taking a variety of classes since we moved to Arizona last summer and is finding lots of great tutorials for her newfound media on YouTube and elsewhere online – alerted me to this carved (presumably clay) dodecahedron by Debi Stoliar. It has 4 faces with a radial starburst pattern and 1 face with a spiral twirled starburst. Way cool!
Over the past few decades, I’ve seen lots of great geometric art, imagery, and more in numerous media, yet occasionally new media forms cross my path in delightful ways. If you search for your favorite geometric form using the search function at the top of the sidebar of this website, you’ll likely find lots of examples. I enjoy learning and discovering new and unique ways artists are transforming geometric ideas into physical and virtual art.
If you have some geometric art (2D, 3D, or otherwise) that we haven’t featured (or haven’t for quite a while) especially if you are using unconventional media, please use our contact form with a link to your art for consideration in the next monthly post on this website and/or our social media (Facebook, YouTube, Twitter a.k.a. X, Pinterest, Instagram, or perhaps another platform we haven’t explored yet! THANKS!
Here are a few dodecahedra (and related shapes) on this website:
